Sprite shrinking

Shrinking (also known as scaling, reduction, zooming...) is a hardware feature of the NeoGeo that reduces the sprites sizes with per-pixel accuracy.

It can be seen as subsampling of the original graphics, there's no smooth interpolation at all.

Vertical shrinking

To do. See Sprites.

Range: $FF is full size, $0 is smallest.

Sprite set to height = 4, graphics intentionally filling 4 tiles (magenta representing size):

If the same sprite is updated to be only 3 tiles high (magenta representing size) without cleaning:

It will shrink this way, showing the garbage yellow tile from the previous setup:

Horizontal shrinking

The horizontal shrinking value is a 4-bit value indicating the final width of the sprite +1 (giving 1 to 16 pixels wide sprites). This value is also set in VRAM, in the SCB2.

Range: $F is full size, $0 is 1 pixel wide.

Skipping of the pixels to render the effect is done by a hardwired lookup table in the GPU. This table is not in the LO ROM.

For each shrinking value, 1 means the pixel will be drawn, 0 means it will be skipped (info from MAME's source, matches the real hardware):

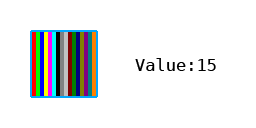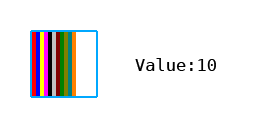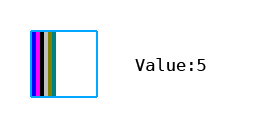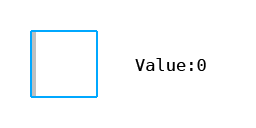
• 0: 0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0 (1 pixel skipped)
• 1: 0,0,0,0,1,0,0,0,1,0,0,0,0,0,0,0
• 2: 0,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0
• 3: 0,0,1,0,1,0,0,0,1,0,0,0,1,0,0,0
• 4: 0,0,1,0,1,0,0,0,1,0,0,0,1,0,1,0
• 5: 0,0,1,0,1,0,1,0,1,0,0,0,1,0,1,0
• 6: 0,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0
• 7: 1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0
• 8: 1,0,1,0,1,0,1,0,1,1,1,0,1,0,1,0
• 9: 1,0,1,1,1,0,1,0,1,1,1,0,1,0,1,0
• A: 1,0,1,1,1,0,1,0,1,1,1,0,1,0,1,1
• B: 1,0,1,1,1,0,1,1,1,1,1,0,1,0,1,1
• C: 1,0,1,1,1,0,1,1,1,1,1,0,1,1,1,1
• D: 1,1,1,1,1,0,1,1,1,1,1,0,1,1,1,1
• E: 1,1,1,1,1,0,1,1,1,1,1,1,1,1,1,1
• F: 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1 (no pixels skipped, full size)

Table logic

The lookup table might not be a real ROM table but a logic function.

For each pixel of the line, WXYZ being the reduction value:

• 0 = W(X+Y)
• 1 = W+X
• 2 = WX
• 3 = W+X+Y
• 4 = WXY
• 5 = W+(XY)
• 6 = W
• 7 = 1
• 8 = WX+WYZ
• 9 = W+X(Y+Z)
• A = WXYZ
• B = W+X+Y+Z
• C = W(X+Y+Z)
• D = W+X+(YZ)
• E = WX(Y+Z)
• F = W+(XYZ)